If we have a lot of redundant data, we may need to perform Dimensionality Reduction on feature quantities.
We can find two very relevant feature quantities, visualize them, and then use a new line to accurately describe the two feature quantities. For example, as shown in Figure 10-1, x1 and x2 are feature quantities with the same nature of the two units, and we can reduce the dimension.
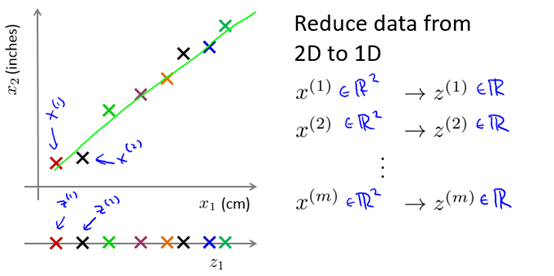
Figure 10-1 An example of 2D to 1D
Also in the 3D to 2D example shown in Figure 10-2, by visualizing x1, x2, and x3, it is found that although the samples are in 3D space, most of them are distributed in the same plane, so we can Through projection, 3D is reduced to 2D.
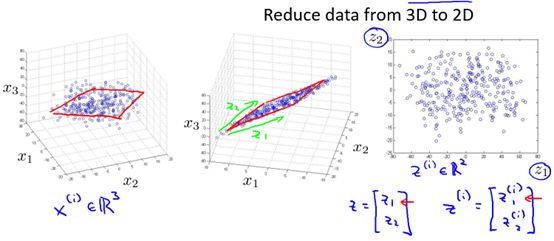
Figure 10-2 A 3D to 2D example
The benefits of dimensionality reduction are obvious. Not only does it reduce the memory footprint, it also speeds up the execution of learning algorithms.
Note that dimensionality reduction simply reduces the number of features (ie, n) rather than reducing the number of training sets (ie, m).
10.1.2 Motivation two: Visualization
We can know, but when the feature dimension is greater than 3, we can hardly visualize the data. So, in order to visualize the data, we sometimes need to reduce it. We can find 2 or 3 representative feature quantities. They (roughly) can summarize other feature quantities.
For example, describe a country with many characteristics, such as GDP, per capita GDP, life expectancy, average household income, and so on. To study and visualize the country’s economic situation, we can select two representative characteristic quantities such as GDP and per capita GDP, and then visualize the data. As shown in Figure 10-3.
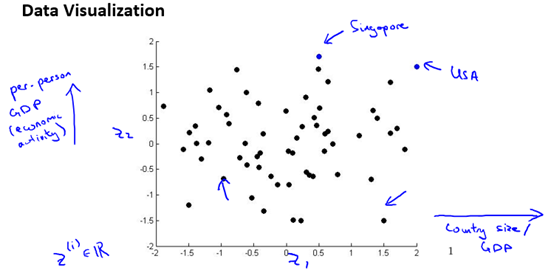
Figure 10-3 A visual example
10.2 Principal Component Analysis
Principal component analysis (PCA) is the most commonly used dimension reduction algorithm.
10.2.1 The problem formulation
First of all, we consider the following questions: How can we use a hyperplane (high-dimensional generalization of a line/plane) to properly express all samples in a sample space in an orthogonal property space (in a rectangular coordinate system for two-dimensional space)?
In fact, if such a hyperplane exists, it should probably have such properties:
Recent reconstitution: the sample points are close enough to the hyperplane;
Maximum separability: The projection of sample points on this hyperplane can be separated as much as possible.
Let's try to understand why these two properties are needed by taking 3D down to 2D as an example. Figure 10-4 shows the distribution of the sample in a 3-dimensional space, where figure (2) is the result of the rotation adjustment of figure (1). In Section 10.1 we default the plane drawn by the red line (may be referred to as the plane s1) to the 2D plane for projection (dimensional dimension reduction). The projection result is shown in (1) in Figure 10-5. It seems to be quite good. So why not project the plane drawn by the blue line (maybe called plane s2)? It can be imagined that the result of the projection with s2 will be as shown in (2) in Figure 10-5.
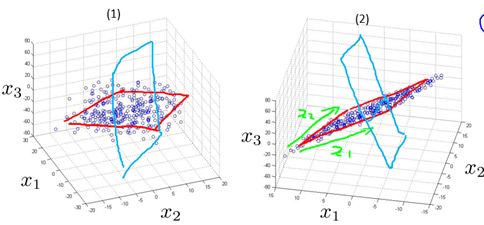
Figure 10-4 Distribution of Samples in 3D Orthogonal Space
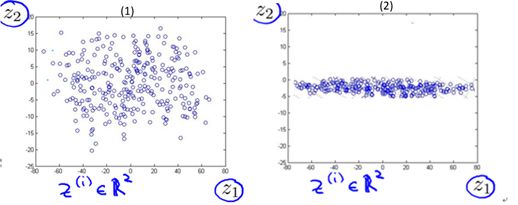
Figure 10-5 Results of the sample projection on a 2-dimensional plane
It can be clearly seen from Figure 10-4 that for the current sample, the s1 plane is better than the s2 plane for the most recent reconstruction (sample is closer to the plane); it can be clearly seen from Figure 10-5. For the current sample, the s1 plane is better than the s2 plane for maximum separability (sample points are more decentralized). It is not difficult to understand that if we choose the s2 plane for projection dimension reduction, we will lose more (a considerable amount) of feature information because its projection result can even be converted into 1 dimension. The projection on the s1 plane contains more information (less loss).
Does this mean that if we reduce from 3D to 1D, we will lose quite a lot of information? Actually not, imagine that if the projection result of plane s1 is similar to that of plane s2, then we can infer that these 3 characteristic quantities are essentially The meaning is roughly the same. So even if you go directly from 3D to 1D, you will not lose more information. It also reflects how well we need to know how to choose to descend to several dimensions (discussed in Section 10.2.3).
To our delight, the above example also illustrates that the recent reconfigurability and maximum separability can be satisfied at the same time. What is even more exciting is that with the goal of recent reconstitution and maximum separability respectively, two equivalent derivation of PCA can be obtained.
In general, the feature quantity is reduced from n-dimensional to k-dimensional:
Targeting the recent reconstructiveness, the goal of the PCA is to find k vectors and project all the samples onto the hyperplane that consists of the k vectors, which minimizes the projection distance (or the projection error projection error is minimal).
Targeting the maximum separability, the goal of the PCA is to find k vectors and project all the samples onto the hyperplane consisting of the k vectors so that the projection of the sample points can be separated as much as possible, that is, the sample points after projection. Maximize variance.
Note: PCA and linear regression are different, as shown in Figure 10-6. Linear regression is targeting the minimum square error sum (SSE) , see section 1.2.4; whereas PCA is the projection (two-dimensional or vertical) distance. Minimal; PCA is completely irrelevant to the marker or predictor, while linear regression is to predict the value of y.
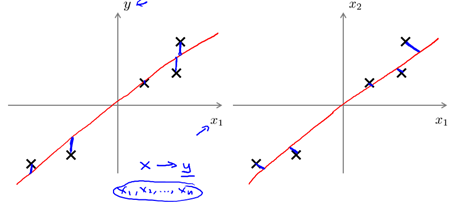
Figure 10-6 PCA is not a linear regression
For the specific derivation process based on the above two goals respectively, see Zhou Zhihua's “Machine Learning†P230. For derivation from the perspective of variance, please refer to Li Hongyi's “Understanding Learning: Principle Component Analysis†(Machine Learning) course (http://speech.ee.ntu.edu.tw/~tlkagk/courses/ML_2017/Lecture/PCA.mp4).
Two equivalent derivation conclusions are: Eigenvalue decomposition of the covariance matrix, sorting the obtained eigenvalues ​​in descending order, and then taking the eigenvectors corresponding to the first k eigenvalues.
among them
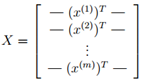
10.2.2 Principal Component Analysis Algorithm
Based on the conclusion given in the previous section, the PCA algorithm is given below.
Input: Training Set: 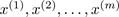
process:
Data preprocessing: Centralize all samples (ie make sample sum 0)
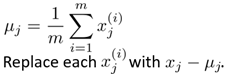
Calculate the sample's covariance matrix (Sigma)
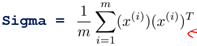
The specific implementation in matlab is as follows, where X is a matrix of m*n:
Sigma = (1/m) * X'* X;
Eigenvalue decomposition of the covariance matrix Sigma obtained in 2
In practice, the singular value decomposition of covariance matrix is ​​usually used instead of eigenvalue decomposition. Implemented in matlab as follows:
[U, S, V] = svd(Sigma); (svd is a built-in function for singular value decomposition in matlab)
Take the feature vector corresponding to the largest k eigenvalues 
In the matlab implementation, Ureduce = 
After the above four steps, the projection matrix Ureduce is obtained. Ureduce can be used to obtain the projected sample values.
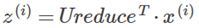
The following summarizes all algorithms for implementing PCA in matlab (assuming data has been centralized)
Sigma = (1/m) * X' * X; % compute the covariance matrix
[U,S,V] = svd(Sigma); %calcul our projected directions
Ureduce = U(:,1:k); % take the first k directions
Z = Ureduce' * X; % compute the projected data points
10.2.3 Choosing the Number of Principal Components
How to choose the value of k (also called the number of principal components)?
First of all, let's think we can use PCA to compress data. How should we decompress it? Or how do you go back to the original sample value? In fact we can use the following equation to calculate the approximate Xapprox of the raw data:
Xapprox = Z * Ureduce (m*n = m*k * k*n )
Naturally, the closer the Xapprox data is to the original data X, the smaller the PCA error. Based on this, a method for selecting k is given below:

With the PCA algorithm, the algorithm for selecting K is summarized as follows:

This algorithm is particularly inefficient. In practical applications, we only need to use the svd() function as follows:

10.2.4 Advice for Applying PCA
PCA is often used to speed up supervised learning algorithms.
The PCA should only obtain the projection matrix Ureduce through the feature set of the training set, instead of a cross-check set or a test set. However, after acquiring Ureduce, it can be applied to cross-examination sets and test sets.
Avoid using PCA to prevent overfitting. PCA only reduces the dimension of feature X and does not consider the value of Y; regularization is an effective way to prevent overfitting.
PCA should not be used at the beginning of the project: It takes a lot of time to select the k value, it is very likely that the current project does not need to use the PCA to reduce the dimension. At the same time, PCA will reduce the feature quantity from n-dimensional to k-dimensional and will certainly lose some information.
Use PCA only when we need to use PCA: The loss of information in dimensionality reduction may be noise to a certain extent, and using PCA can have a denoising effect.
PCA is usually used to compress data to speed up algorithms, reduce memory usage or disk usage, or for visualization (k=2, 3).
AURORA SERIES DISPOSABLE VAPE PEN
Zgar 2021's latest electronic cigarette Aurora series uses high-tech temperature control, food grade disposable pod device and high-quality material.Compared with the old model, The smoke of the Aurora series is more delicate and the taste is more realistic ,bigger battery capacity and longer battery life. And it's smaller and more exquisite. A new design of gradient our disposable vape is impressive. We equipped with breathing lights in the vape pen and pod, you will become the most eye-catching person in the party with our atomizer device vape.The 2021 Aurora series has upgraded the magnetic suction connection, plug and use. We also upgrade to type-C interface for charging faster. We have developed various flavors for Aurora series, Aurora E-cigarette Cartridge is loved by the majority of consumers for its gorgeous and changeable color changes, especially at night or in the dark. Up to 10 flavors provide consumers with more choices. What's more, a set of talking packaging is specially designed for it, which makes it more interesting in all kinds of scenes. Our vape pen and pod are matched with all the brands on the market. You can use other brand's vape pen with our vape pod. Aurora series, the first choice for professional users!
We offer low price, high quality Disposable E-Cigarette Vape Pen,Electronic Cigarettes Empty Vape Pen, E-cigarette Cartridge,Disposable Vape,E-cigarette Accessories,Disposable Vape Pen,Disposable Pod device,Vape Pods,OEM vape pen,OEM electronic cigarette to all over the world.






Disposable Pod Vape,Disposable Vape Pen,Disposable E-Cigarette,Electronic Cigarette,OEM vape pen,OEM electronic cigarette.
ZGAR INTERNATIONAL(HK)CO., LIMITED , https://www.zgarpods.com