Abstract: Probability distribution is common in many areas, including insurance, physics, engineering, computer science, and even social sciences such as psychology and medicine. It is easy to apply and has a wide range of applications. This article focuses on six important distributions that are often encountered in everyday life and explains their application.
01 Introduction
Suppose you are a teacher at a university. After checking your homework for a week, you scored all the students. You handed the scored papers to the university's data entry staff and told him to create a spreadsheet containing all student grades. But this person only stores the results, but does not include the corresponding students.
He made another mistake and skipped a few things in a hurry, but we didn't know who lost the results. Let's see how to solve this problem.
One way is to visualize the results to see if you can find a trend in the data.
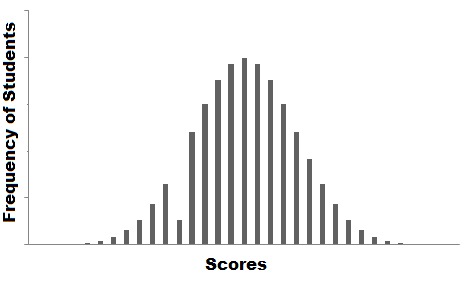
The graph shown above is called the frequency distribution of the data. There is a smooth curve, but have you noticed an abnormal situation? The frequency of the data is unusually low within a certain score range. Therefore, the most accurate guess is that the value is lost, resulting in a depression in the distribution.
This process shows how you can use data analytics to try to solve real-life problems. For any data scientist, student, or practitioner, distribution is a concept that must be known, which provides the basis for analysis and reasoning statistics.
Although probability provides us with mathematical calculations, distribution can help us visualize what is happening internally.
In this article, I will introduce some important probability distributions and explain them clearly and comprehensively.
Note: This article assumes that you already have a basic knowledge of probability. If not, you can refer to this article on the basis of probability.
02 Common data types
Before we get into the details of the distribution, let's take a look at what kind of data we will encounter. Data can be divided into discrete and continuous.
Discrete data: As the name suggests, only the specified values ​​are included. For example, when you cast a dice, the output may only be 1, 2, 3, 4, 5, or 6, and 1.5 or 2.45 may not appear.
Continuous data: Any value can be taken within a given range. The range can be limited or unlimited. For example, the girl's weight or height, the length of the journey. The girl's weight can be 54 kg, 54.5 kg, or 54.5436 kg.
Now let's start learning the type of distribution.
03 Type of distribution
Bernoulli distribution
We start with the simplest distribution of the Bernoulli distribution.
The Bernoulli distribution has only two possible outcomes, 1 (success) and 0 (failure). Therefore, the random variable X with Bernoulli distribution can take a value of 1, which is the probability of success, which can be expressed by p or a value of 0, that is, the probability of failure, represented by q or 1-p.
The probability mass function is given by: px(1-p)1-x, where x € (0, 1). It can also be written as:
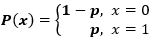
The probability of success and failure is not necessarily equal. Here, the probability of success (p) is different from the probability of failure. So, the chart below shows the Bernoulli distribution of the results between us.
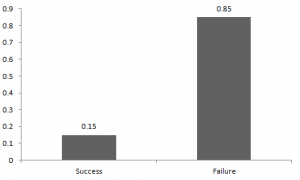
Here, the probability of success = 0.15, the probability of failure = 0.85. If I hit you, I might expect you to call me back. The basic expected value of any distribution is the average of the distribution. The expected value of the random variable X from the Bernoulli distribution is:
E(X) = 1*p + 0*(1-p) = p
The variance between the random variable and the binomial distribution is:
V(X) = E(X2) – [E(X)]2 = p – p2 = p(1-p)
There are many examples of Bernoulli distribution, such as whether it is raining, if it rains, it means success, if it doesn't rain, it means failure.
Evenly distributed
For the dice, the result is 1 to 6. The probability of getting any one result is equal, which is the basis for a uniform distribution. Unlike the Bernoulli distribution, the n number of all possible outcomes of a uniform distribution are also equal.
If the variable X is evenly distributed, the density function can be expressed as:

The evenly distributed curve looks like this:

As you can see, the shape of the evenly distributed curve is a rectangle, which is why the uniform distribution is also called a rectangular distribution. Among them, a and b are parameters.
The number of bouquets sold daily by the florist is evenly distributed, up to a maximum of 40 and a minimum of 10. Let's calculate the probability that the daily sales will be between 15 and 30.
The probability of daily sales between 15 and 30 is (30-15)*(1/(40-10)) = 0.5
Similarly, the probability of a daily sales volume greater than 20 is = 0.667
The mean and variance of the X that follows a uniform distribution are:
Average -> E(X) = (a+b)/2
Variance -> V(X) = (ba)2/12
The standard uniform density parameters a = 0 and b = 1, so the standard uniform density is given by:
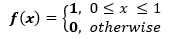
Binomial distribution
Let's take a look at the example of playing cricket. Suppose you won a game today, which represents a successful event. You are more than one, but you lose. If you win a game today, it doesn't mean you will win tomorrow. Let's assign a random variable X to indicate the number of wins. What is the possible value of X? It can be any value, depending on how many times you roll the coin.
There are only two possible outcomes, success and failure. Therefore, the probability of success = 0.5, the probability of failure can be easily calculated: q = p – 1 = 0.5.
A binomial distribution is a distribution with only two possible outcomes, such as success or failure, gain or loss, win or defeat, and the probability of success and failure for each attempt is equal.
The results may not necessarily be equal. If the probability of success in the experiment is 0.2, the probability of failure can be easily calculated as q = 1 - 0.2 = 0.8.
Each attempt is independent, as the result of the previous throw cannot determine or affect the outcome of the current throw. An experiment with only two possible outcomes and repeated n times is called a binomial. The parameters of the binomial distribution are n and p, where n is the total number of trials and p is the probability of success for each trial.
Based on the above description, the attributes of the binomial distribution include:
1. Each test is independent.
2. There are only two possible outcomes in the trial: success or failure.
3. A total of n identical tests were performed.
4. The probability of success and failure of all trials is the same. (The test is the same)
The mathematical representation of the binomial distribution is given by:
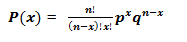
The success probability is not equal to the binomial distribution of the probability of failure:
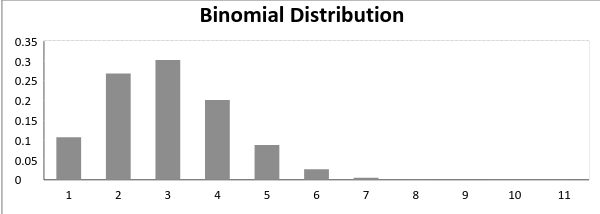
Now, when the probability of success = the probability of failure, the binomial distribution is as follows
The mean and variance of the binomial distribution are given by:
Average -> μ = n*p
Variance -> Var(X) = n*p*q
Normal distribution
The normal distribution represents the state of operation of most situations in the universe. A large number of random variables have been shown to be normally distributed. Any one of the distributions can be called a normal distribution as long as it has the following characteristics:
1. The mean, median, and pattern of the distribution are consistent.
2. The distribution curve is bell-shaped and is symmetric about the line x = μ.
3. The total area under the curve is 1.
4. Half of the value is on the left side of the center and the other half is on the right side.
The normal distribution is very different from the binomial distribution. However, if the number of trials is close to infinity, their shape will become very similar.
The value of the random variable X following a normal distribution is given by:
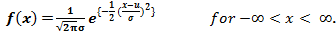
The mean and variance of a normally distributed random variable X are given by:
Mean -> E(X) = μ
Variance -> Var(X) = σ^2
Among them, μ (average) and σ (standard deviation) are parameters.
The graph of the random variables X to N (μ, σ) is as follows.
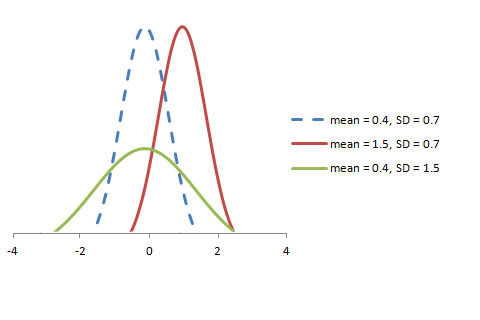
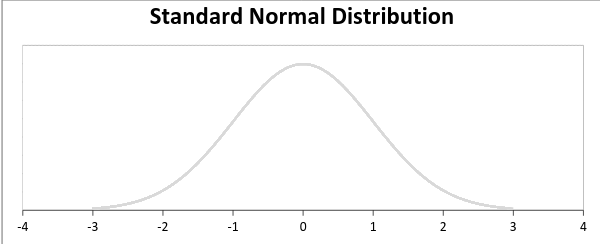
The standard normal distribution is defined as a distribution with an average value equal to 0 and a standard deviation equal to 1:

Poisson distribution
Suppose you work in a call center. How many calls will you receive in a day? It can be any number. The total number of calls per day in a call center can now be modeled using a Poisson distribution. Here are some examples:
1. The number of emergency calls recorded by the hospital in one day.
2. The number of thefts reported in a given area in a day.
3. The number of customers arriving at the salon within one hour.
4. Number of suicides reported in a particular city.
5. The number of errors printed on each page of the book.
The Poisson distribution is suitable for situations where events occur at random times and spaces, where we only focus on the number of times the event occurred.
When the following assumptions are valid, they are called ** Poisson distribution**
1. No successful event should affect another successful event.
2. The probability of success in a short period of time must be equal to the probability of success in a longer interval.
3. When the time interval becomes smaller, the probability of success in the interval time tends to zero.
These symbols are used in the Poisson distribution:
λ is the rate at which the event occurs
t is the length of the interval
X is the number of events in this interval.
Among them, X is called Poisson random variable, and the probability distribution of X is called Poisson distribution.
Let μ denote the average number of events in the interval of length t. Then, μ = λ*t.
The X of the Poisson distribution is given by:

The average value μ is a parameter of this distribution. μ is also defined as λ times the length of the interval. The Poisson distribution diagram is as follows:

The figure below shows the offset of the curve as the average increases:
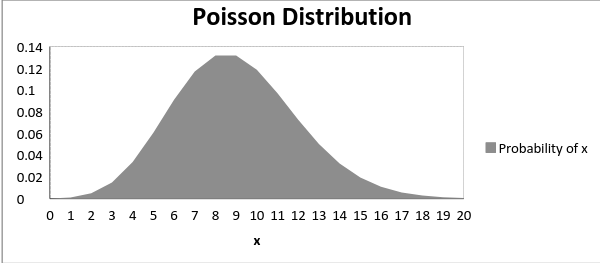
It can be seen that as the average value increases, the curve moves to the right.
The mean and variance of X in the Poisson distribution:
Mean -> E(X) = μ variance -> Var(X) = μ
index distribution
Let us look at the example of the call center again. What is the time interval between different calls? Here, the exponential distribution simulates the time interval between calls.
Other similar examples are:
Subway arrival time interval
2. Time to arrive at the gas station
3. Air conditioning life
Exponential distribution is widely used for survival analysis. From the life expectancy of the machine to the life expectancy of humans, the exponential distribution can successfully provide results.
Random variable X with an exponential distribution** of **:
f(x) = { λe-λx, x ≥ 0
The parameter λ>0 is also called the rate.
For survival analysis, λ is referred to as the failure rate of the device at any time t, assuming it has survived to time t.
The mean and variance of the random variable X following the exponential distribution are:
Average -> E(X) = 1/λ
Variance -> Var(X) = (1/λ)2
In addition, the higher the rate, the faster the curve drops, the slower the rate, the flatter the curve. The diagram below illustrates this very well.
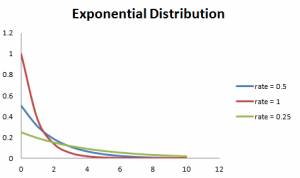
To simplify the calculation, some formulas are given below.
P{X≤x} = 1 – e-λx corresponds to the area under the curve to the left of x.
PP{X>x} = e-λx corresponds to the area under the curve to the right of x.
P{x1-λx1 - e-λx2, corresponding to the area under the density curve between x1 and x2.
P{x1-λx1 - e-λx2 corresponds to the area under the curve between x1 and x2.
04 Relationship between various distributions
The relationship between Bernoulli and the binomial distribution
1. The Bernoulli distribution is a special case of a binomial distribution with a single test. 2. The Bernoulli distribution and the binomial distribution have only two possible outcomes, success and failure. 3. Bernoulli distribution and
Binomial distributions have independent trajectories.
The relationship between Poisson and binomial distribution
The Poisson distribution is the limit case of the binomial distribution if the following conditions are met:
1. The number of tests is infinite or n → ∞.
2. The probability of success for each trial is the same, infinitely small, or p → 0.
3. np = λ, which is finite.
Normal distribution
A normal distribution is another form of restriction of a binomial distribution if the following conditions are met:
1. The number of trials is infinite, n → ∞.
2. Both p and q are not infinitely small.
The normal distribution is also the limit of the Poisson distribution of the parameter λ → ∞.
The relationship between the exponent and the Poisson distribution
If the time between random events follows an exponential distribution with a rate of λ, the total number of events within the length of time t follows a Poisson distribution with the parameter λt.
05 Conclusion
Probability distribution is common in many areas, including insurance, physics, engineering, computer science, and even social sciences such as psychology and medicine. It is easy to apply and has a wide range of applications. This article focuses on six important distributions that are often encountered in everyday life and explains their application. Now you have been able to identify, correlate and distinguish between these distributions.
SDRam 4gb ddr3 laptop ram 8gb memory rams factory direct
OSCOO DDR3 memory module products, through rigorous testing andscreening, select better memory particles, improve product compatibility and stability. Provides a better processing environment for large games. With low heating rate and low power consumption.
OSCOO DDR3 desktop memory will be the first choice for consumers to install.
The SPDs are programmed to JEDEC standard latency DDR3-1600 timing of 11-11-11 at 1.5V. Each 240-pin DIMM uses gold contact fingers.
DDR3 Memory Ram module laptop,DDR3 1333 2GB/4GB/8GB ddr3 ram 4gb 1600mhz Notebook,DDR3 ram 4gb So-dimm 1600MHz PC3-12800
MICROBITS TECHNOLOGY LIMITED , https://www.hkmicrobits.com