Quantum Machine Learning (Quantum ML) is an interdisciplinary subject between quantum mechanics and machine learning. Between the two is a symbiotic relationship, we can use the power of quantum computing to generate quantum versions of machine learning algorithms and apply classical machine learning algorithms to analyze quantum systems.
In this article, Reena Shaw, a master of computer science, will bring you to the quantum machine learning with a metaphor of language and image.

â–³ Author Reena Shaw
At the Microsoft Ignite conference in 2017, Microsoft CEO Satya Nadella used the image of the corn maze to explain the difference between a classic computer and a quantum computer.
In order to find the exit of the maze, the classic computer first opens a search path and returns along the original path after encountering an obstacle. Then explore the new road again until you get back or find the right exit. Although a result can be found eventually, this method is quite time consuming.
In contrast, quantum computers "unlock the magical parallelism. They also explore every path in the corn maze." Therefore, quantum computers may exponentially reduce the number of steps to solve the problem.
This parallelism originated from theories of "qubit", "superposition" and "entanglement" in quantum physics.
The magic of this is far more than that, and you have to continue to look down.

Quantum computing
Quantum
Quantum is the smallest possible unit of any physical entity (such as energy and mass). In 1900, Max Planck, a German physicist and founder of quantum mechanics, proposed that at the atomic and subatomic levels, the energy of an object is contained in discrete data packets called quanta.
Wave-particle duality is a feature of quantum particles. It means that microscopic particles are sometimes volatility based on different environments, and sometimes exhibit particle properties.
The characteristic of quantum theory is to find the probability that a given point x exists in space, not its exact position.
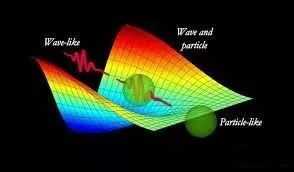
â–³ Light has the dual nature of examples and waves
Qubit (Qubit)
Classical computers perform operations through classic "bits". These bits are either 0 or 1, and quantum computers borrow "qubits."
Qubits can be represented as electrons and photons that orbit around the nucleus. The polarization state of a photon and the spin state of an electron can be represented by |1> and |0>, respectively.
Superposition
Qubits exist in both 0 and 1. This phenomenon is called "superposition."
Although particles can exist in multiple quantum states, once we have determined the energy or position of the particles, the superposition disappears and it can only exist in one state.
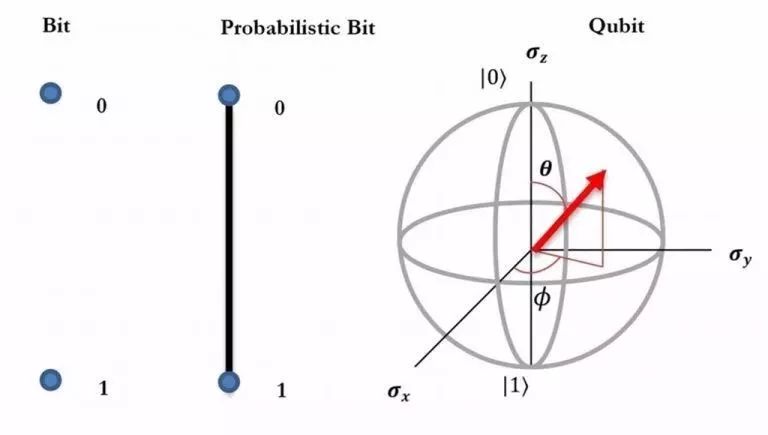
The â–³ qubit is defined as a pair of complex vectors pointing to a point in the unit sphere. In general, the qubits pointing directly above (positive axis) are represented as column vectors |0>, and the qubits pointing down (negative axis) are row vectors |1>.
Entanglement
"Quantum entanglement" refers to the interaction between quantum particles. Even if the particles are far apart, they still interact and cross-reference, not independent.
When measuring, if a pair of entangled quantum is determined to be in the downward spin state (low energy state), then when the electron is in line with its magnetic field, the state is passed to another related arrow. An example of the relative spin state.
Quantum entanglement allows qubits that are far apart to interact with each other in time.
After talking about these four basic concepts, there may be a question, how does quantum computing release huge parallelism?
The two interacting classical bits have four states, 00, 01, 10 or 11. The two components of each message (the first bit and the second bit) combine to represent only the binary structure at a given time. Adding more bits to a normal computer still represents a binary structure.

â–³ The qubit in the superposition before measurement has the probability of “spin up†and “spin downâ€
A qubit can have both states 0 and 1. Therefore, two interacting qubits can be simultaneously stored as four binary structures. In general, 'n' qubits can represent '2n' classic binary structures at the same time.
Therefore, a 300 qubit quantum computer can simultaneously explore 2n possible results, thus bringing great parallelism. Therefore, adding more qubits to a quantum computer can double the computational power.
At present, our technology is not able to achieve quantum computers in the true sense, because adding more qubits and processing subatoms requires a low temperature environment below -452 degrees Fahrenheit.
Therefore, Microsoft expanded its Microsoft Azure cloud computing resources through the quantum simulator LIQUi|>simulating 40 qubit operations.
Quantum computing solves professional scientific problems such as molecular modeling, generation of high temperature superconductors, drug modeling and testing, molecular selection, and the manufacture of organic batteries. It is not the best choice for general-purpose tasks such as watching videos or writing Word documents.
Quantum machine learning
Quantum version machine learning algorithm
Find the eigenvalues ​​and eigenvectors of a giant matrix:
One way is that one of the methods of performing the classical PCA (principal component analysis) algorithm is to take the eigenvalue decomposition of the data covariance matrix. However, this is not very effective in the case of high dimensional data.
An unknown low-density matrix quantum PCA can reveal quantum features associated with large eigenvalues, exponentially increasing in speed compared to classical algorithms of linear scale.
Find neighbors on quantum computers
The quantum algorithm for calculating neighbors using supervised learning and unsupervised learning is to set the upper limit of the number of queries to the input data required to calculate the distance index, such as the Euclidean distance and the inner product.
Related paper address: https://arxiv.org/abs/1401.2142
Quantum method to improve the Higgs boson experiment
In the Higgs Boson experiment, the Higgs boson particles decayed into a collection of small particles almost immediately after they were produced. The most common attenuations are roughly the following:
In solving the "Higgs particle signal against background" machine learning optimization problem, many researchers try to separate the signal from the background. In addition, the combination of quantum annealing and classical annealing is most beneficial to machine learning methods.
A quantum algorithm for solving linear equations:
Some quantum techniques can also work in subroutines that solve machine learning problems, such as matrix inversion.
This problem can be expressed as an A matrix and a vector b want to find the vector x satisfies Ax=b. In order to solve linear equations with quantum algorithms, we do not need to understand the x solution itself, but an expectation of x for some operator approximations.
Machine learning analysis quantum system
Classic machine learning algorithms have been utilized to control and display benchmark systems for quantum phenomena, such as Bose–Einstein condensate (BEC).
BEC is a state of matter in which the dilute gas of a boson atom is cooled to near absolute zero, and most bosons are in a ground state.
The quantum effect will disappear at the macro level, but BEC shows the quantum effect at the macro level. Scientists have invented a machine learner to discover the optimal evaporation ramp to create high-quality BEC.
In addition, we need to crack the process of optimizing BEC, because the learned machine learning model determines which parameters are essential in the BEC creation process.
In the design of quantum devices, many building blocks are done with the help of machine learning algorithms.
Machine learning algorithms play an important role in many issues, such as:
Detect quantum change points:
A quantum device can emit particles of different states in a specific state. To detect this change in state, the scientists compared the performance of the local measurements with the performance of the overall measurements.
Local measurement: measure the state of each particle reaching the detector.
Overall measurement: the last measurement when all particles arrive at the detector
For local measurements, Masahide Sasaki constructed a classification of an unknown state system as a form of supervised learning in a previous paper. Finally, the researchers found that overall measurements performed better than local measurements when detecting sudden quantum changes.
Paper address: https://arxiv.org/abs/quant-ph/0202173
Binary classification of qubit states:
Scientists have trained a quantum learning machine that divides the state of qubits into zeros and ones. The growth of classical memory grows logarithmically with the number of training qubits, even under a sufficiently large training set of compositional changes. It can also perform very well.
Quantum decoherence:
When the equivalent subsystem is not completely isolated, some system information is lost in the environment, resulting in the loss of quantum behavior, which is called quantum decoherence.
Machine learning techniques can be used to understand more random phase shifting processes on qubits to predict quantum decoherence and stabilize the future phase shift of qubits.
Recreate the value of the thermodynamically observable:
The thermodynamically observable properties of energy, specific heat and magnetism can be reproduced using the recursive neural network of the Boltzmann machine. The machine is trained using a data set generated by Monte Carlo sampling.
2-in-1 Tablet, tablet with keyboard, android tablet with case tablet with pen, mini laptop
C&Q Technology (Guangzhou) Co.,Ltd. , https://www.gzcqteq.com